確率は収束しない、あなたが期待するようには

カジノにルーレットってありますよね。
ルーレットは数字に賭けることもできますが、赤と黒の二択に賭けることもできます。

ずっと前にテレビで見たのですが、この二択で、何度か連続で同じ色が出た後に反対の色に賭けると当たりやすいのだとか。なぜなら確率は収束するからッ！！！

例えば5回連続で赤が出たあと、次もまた赤の確率は

というわけです。どう思いますか？

ええ、ええ、はい。
最初の一回とやっていることが一緒なのに最後の一回の確率が3%になるわけありませんよね。いわゆる同様に確からしいというやつです。もちろん、次の試行で赤がでる確率は50%なのですが…(ルーレットの場合は、正確には0があるのでもう少し低いけどね！🤪)こうした確率の基本は、多分中学校くらいで教わると思います。

でもそれじゃいつになっても確率が収束しないじゃん？

ここまで5回連続で赤が出ているのに、次の確率も50%じゃあ、いったいどうやって50%に収束するんだッ！いつか黒に偏らないとおかしいじゃねぇか！！！

…というのは、確率の収束を誤解しています。
確率の収束とは、試行の結果が同じ回数になることではないのです。
大数の法則により、全体からみれば、これまでの偏りが薄まってみえるというだけです。

つまり次はあやまった解釈です。

確率は収束するはずだから次こそは…という考え方はこれと同じ考え方ですね。
（次こそは…と考えてしまうのは、サンクコスト（コンコルド効果

¹

）で補強されてる場合もあるかと思います。）

正しくは、

…と50%に近づいていくという話です。確率の収束とは、このあと確率通りに出れば、全体としては確率の値に近づくと言っているだけなのです。

どれだけ試行を増やしても、次の試行は50%の確率であることはかわらないというわけです。
それぞれの試行が独立している限り、次の出目を予測することはできません。

気持ち的にはわからなくもないですけどね。

確率より運が悪くなってしまったときは、サンクコストを回収しようとせず、「もう一度同じ確率で同じことが起きる」、と考えなければ泥沼化してしまいます。

逆に、運が良いときは、この先に良かった分がだけ悪くなるということはないわけですから、素直に喜びましょう。ツキがキていると考えて負けるまで粘ってはいけません！

確率の収束を正しく活用するには？

確率の収束の活用としては、どのくらいの回数の試行でどのくらい確率が収束していくかを計算しておくことです。あらかじめ覚悟してはじめるたり、結果に納得することができます。

ガチャの確率分布の計算（一般のガチャ用） – 高精度計算サイト

上記のサイトは、二項分布の確率密度関数を用いてそれぞれのまとまった試行回数での出現確率が計算できます。スマホゲームのガチャの確率が想定されていますが、ルーレットなど同じ試行を繰り返すような、同じ仕組みのゲームであれば応用できます。

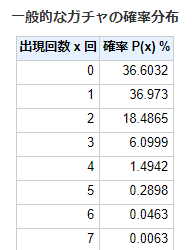
上の画像は上記のサイトを使って1%の確率の試行を100回繰り返したときのそれぞれの結果の確率です。

たとえば100回ではきれいに収束せずに、一度も1%を引けない確率、つまり100回引いても0回になる確率は36.6032%です。1%程度の確率では三人に一人以上が100回引いても一度も引けません。

ちょうど1回、つまり確率がきれいに収束したとも考えられる人の割合は約36.973%です。同じく三人に一人くらいですね。

その一方で、2回以上引ける人が18%程度います。

注意しなければいけないのは、もちろん、50回目までに引けなかったら、残りの50回で引ける確率は計算し直さなければならないことです。たとえば、50回引いて計算し直したら、残りの50回で1%の当たりが引けない確率は最初の50回と同じ約60.5%です。

このように、確率の収束は、収束する確率を計算することで真価を発揮します。ギャンブルと言えど、賢い人に有利なのは変わらないということですね。計算をして正しい理解で望む、果たしてそれはもはやギャンブルと呼べるのか？という疑問が生まれてしまいそうですが😅

最後に

確率は収束するッ！！！ニートは就職しないッ！！！